Mechanisms: The Puzzle of Rotational to Linear(ish) Motion

In the world of Physics and engineering, there are certain mechanisms that can be very useful when it comes to the transformation of different types of motion. Motion along a straight line can be transformed into angular motion, and vice versa. After reviewing the various provided sources about mechanisms that convert rotational motion into linear motion, one mechanism in particular stood out to me: the elliptical gear pair.

Image from http://kmoddl.library.cornell.edu/model.php?m=689

The elliptical gear works by transforming steady axis motion into non-steady axis motion on an adjacent gear. In the above picture, the elliptical shape of the gears themselves is what enables this transformation. The gears can actually change the rate at which they spin depending on where they are in contact with each other. The ability to alter the rate of rotation was very intriguing to me, as it opened up all sorts of timing possibilities for different products. For example, if someone wanted a cranked door to open in a given amount of time, they could use an elliptical gear pair and save the material it would take to make a large, circular gear to achieve the same time difference. 

This variation in speed, as well as position of the gears, makes them extremely versatile. Elliptical gears have contributed to various flow rates in pumps and flowmeters. * The fixed points in an elliptical pair is constant, and as a result, the speed varies to keep this distance between the points equal at all orientations.

Image from http://www.cunningham-ind.com/ellipt.htm

The gears do not have to be the same size (or same shape, though that's an entirely different category of mechanisms) for this to work. Despite their oblong appearance, elliptical gears will rotate about their foci ('center') in a manner that allows them to stay in contact and their foci to be equidistant to each other in all orientations.

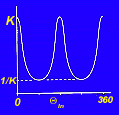Speed variation in elliptical gear pair

This change in orientation to maintain the distance caused the speed variations along the edge of the gears, modeled here. It can range from as high as K to as low as 1/K, where K is the maximum gear ration possible based on the size of the gears. *












*for more information, see http://www.cunningham-ind.com/ellipt.htm